Breaking Project Euler with GPUs
Table of Contents
I recently dove into GPU programming through a combination of the fantastic Hands-On OpenCL course1 and PyOpenCL’s documentation.2 While looking for ways to practice, I decided a Project Euler problem would be a great candidate. After finishing up, I was pleasantly surprised with how simple it was to implement GPU computation and with the insane performance boost I saw from even a trivial use of the techniques. If you’ve dabbled with functional programming before, I think you’ll find GPU programming to be shockingly intuitive.
Why GPU Programming? #
GPUs have changed form several times throughout their history, but they’ve always had a very specific goal: to be really really fast at processing image data. Modern GPUs do this better than CPUs through a fairly simple strategy - having thousands of weaker cores instead of a handful of stronger ones. For example, my Intel Core i5-10600K CPU has 6 cores running at 4.10 GHz, while my EVGA RTX 3700 GPU has 5888 CUDA cores running at 1.815 GHz.
This strategy works for graphics because rendering images is considered an embarrassingly parallel problem. Calculating the result of each pixel does not (usually) depend on the result of another pixel. And those individual calculations are computationally light, relatively speaking. Thousands of slow calculations in parallel are much much better than tens of faster ones. Of course, image rendering isn’t the only embarrassingly parallel problem. Any problem that fits these criteria could potentially benefit from GPU computation.
Problem Overview #
I chose to revisit Project Euler’s Problem 43 - Sub-string divisibility. This was a problem that I initially solved through a very slow bruteforce method before I learned the more correct solution. This problem had all the right requirements to benefit from GPU computation: a very large workload that you can separate into independent tasks. I felt it would be fun to solve this problem using my initial “caveman brain” solution, but this time using a modern club.
The good thing about Project Euler is that they impose no limitations on how you solve their problems. (except for outright copying a solution) Their problems are designed according to a “one-minute rule”, meaning every problem has a technique that allows even a modest computer to solve it within a minute. However, this is primarily a design criterion for them. While it is a good goal, nothing requires you to abide by this rule. If your technique takes days to complete, but it still outputs the correct solution, you’re fully allowed to submit that answer.
All of this is to say that every Project Euler problem has an “intended” solution that’ll get you the answer relatively quickly, even sequentially using a modest computer. But of course, that is not what we’re here to do today. Our goal is to implement the least-elegant solution possible and force it to run under one minute through the power of GPU computation.
Problem 43’s description is:
The number, 1406357289, is a 0 to 9 pandigital number because it is made up of each of the digits 0 to 9 in some order, but it also has a rather interesting sub-string divisibility property.
Let d1 be the 1st digit, d2 be the 2nd digit, and so on. In this way, we note the following:
- d2 d3 d4 = 406 is divisible by 2
- d3 d4 d5 = 063 is divisible by 3
- d4 d5 d6 = 635 is divisible by 5
- d5 d6 d7 = 357 is divisible by 7
- d6 d7 d8 = 572 is divisible by 11
- d7 d8 d9 = 728 is divisible by 13
- d8 d9 d10 = 289 is divisible by 17
Find the sum of all 0 to 9 pandigital numbers with this property.
Solving the Problem Normally #
Before we dive into the GPU solution, let me demonstrate the bruteforce solution using the CPU to lay the foundation for how much a GPU helps. If you attacked this problem with the intent to do as little optimization as possible, one approach would be to:
- Identify the range of numbers to test.
- Determine which numbers are pandigital.
- Determine if those numbers also have the substring divisibility property.
- Add up all numbers that pass these two requirements.
Step 1 - Identify the Search Space #
Since it’s not feasible to search ALL numbers, the first issue is how to define our search space. We can see that all pandigital numbers are 10 digits, so they should never be greater than 9,999,999,999. If we assume leading zeros are allowed, then our starting search space is 0 → 9,999,999,999.
If we stick to GPU computation, this search space would be viable. However, this would make the sequential version far too slow—on the order of several hours of runtime. Since I want something to compare the GPU version to, (and don’t intend to wait hours to measure runtimes) we’ll apply one more optimization. We can see that the sum of the numbers 0 → 9 is 45, which is divisible by 9. Through this property, we can determine that all zerofull restricted pandigital numbers are also divisible by 9.3 Knowing this property, we can further reduce our search space 9-fold if we only test numbers divisible by 9. This reduces the numbers we need to search to “only” 1,111,111,111.
Step 2 - Identify Pandigital Numbers #
Since the example includes a number with a zero, we can confirm that they are asking for zerofull pandigital numbers. And because the sub-string divisibility property uses ten digits, we can also assume that the numbers are restricted, meaning each digit only appears once. So, the goal is to determine if a number contains the digits 0 through 9 and that each digit appears only once.
Our first step is to separate the number into its individual digits. The simplest way to do this in Python is to just convert the number into a string using str(num). Then we can simply iterate through the string to read the individual digits. While you could extract the digits computationally, it is actually faster to convert the number since the built-in “number to string” function is written in C. To demonstrate this, I wrote two different functions that extract digits from an integer. One does this computationally and the other uses string conversion. As you can see, the one using string conversion is noticeably faster.
import timeit
import random
def get_digits_computational(n):
digits = []
while n > 0:
digits.append(n % 10)
n //= 10
return digits
def get_digits_string_conversion(n):
return str(n)
# Randomly generate one million ten-digit numbers
test_numbers = [random.randint(1_000_000_000, 9_999_999_999) for _ in range(1_000_000)]
# Measure performance of both methods
print(f"Computational: {timeit.timeit(lambda: [get_digits_computational(n) for n in test_numbers], number=1)}")
print(f"Strings: {timeit.timeit(lambda: [get_digits_string_conversion(n) for n in test_numbers], number=1)}")
$ python3 get_digits_tests.py
Computational: 0.9255661
Strings: 0.21739010000000003
Don’t take this to mean “built-in function will always be faster”. For completeness’ sake, I tested a third function that converts the number to a string and then converts each character back into an integer. This method is actually slower than the fully-computational method. So if you needed to do calculations on the individual digits, the computational method would be better. However, it’s also not that much slower than the computational method, so don’t fall into the micro-optimization trap.
def get_digits_string_conversion_and_back(n):
return [int(d) for d in str(n)]
print(f"Strings and Back: {timeit.timeit(lambda: [get_digits_string_conversion_and_back(n) for n in test_numbers], number=1)}")
$ python3 get_digits_tests.py
Strings and Back: 1.2517554000000002
Now that we can get the individual digits, our next step is to make sure they each only appear once. One possible way to do this is to loop through the digits and track the digits we see. If we find a digit that we’ve already seen before, then we know that the number is not pandigital. If we check every digit and find no duplicates, then we know that the number is pandigital. We also need to make sure the number we’re testing has exactly 10 digits. Without this test, we may pass invalid numbers such as 1234 because we’re just checking if each digit only appears once. The final validation function looks like this:
def is_pandigital(n: int) -> bool:
# Separate the number into its individual digits
n_str = str(n)
# This number must have exactly 10 digits to be valid
if len(n_str) != 10:
return False
# Ensure each digit only appears once
previously_seen = set()
for digit in n_str:
# If we see any digit twice, this is an invalid number
if digit in previously_seen:
return False
else:
previously_seen.add(digit)
# If we never see a digit twice, this is a valid number
return True
Step 3 - Identify Substring Divisible Numbers #
The biggest challenge for this step is extracting the substrings from the number. Thankfully, Python has a pretty intuitive system for substrings. The only caveat is that we can have to do this on strings. So we have to convert to a string, extract the substring, and then convert back into an integer. While this is a lot of converting, it’s likely faster to just do these conversions since they all use built-in functions. To perform the divisibility tests, we will create a list of the different substrings and then compare them to their respective divisors. If any of those substrings fail the divisibility test, then we know that the number is not substring divisible. But if we make it through every test without failing, then we know that the number is substring divisible. The final test function looks like this:
def is_substring_divisible(n: int) -> bool:
# Extract the 7 substrings from the input number
n_str = str(n)
substrings = [int(n_str[i+1:i+4]) for i in range(7)]
# Test each substring against its respective divisor
divisors = [2, 3, 5, 7, 11, 13, 17]
for s, d in zip(substrings, divisors):
# If any substring fails, this number is invalid
if s % d != 0:
return False
# If every substring passes, this number is valid
return True
Step 4 - Calculate the Solution #
Single-threaded CPU #
Now we’re home free! All we need to do is combine the previous 3 steps into a complete Python program to calculate the solution:
def bruteforce() -> int:
solution = 0
for n in range(0, 10_000_000_000, 9): # Step 1
# Steps 2 and 3
if is_pandigital(n) and is_substring_divisible(n):
# Step 4
solution += n
return solution
def main():
print(f"Bruteforce CPU")
solution = bruteforce()
if solution == ███████████:
print(f"Correct solution!")
if __name__ == "__main__":
main()
Project Euler technically allows me to include the solution here since it’s within the first 100 problems. But, I still would like to keep with the spirit of their intent and not outright post the solution.
To measure the total runtime for each solution, we’ll be using the following PowerShell script. For these first few solutions, it’ll only measure the execution once and then display that runtime in seconds. But when we start achieving runtimes below 10 seconds, then it’ll start calculating averages across many trials.
# First Test Run
$runtimes = [System.Collections.ArrayList]@();
$runtimes.Add(
@(Measure-Command {& python src/p43.py | Write-Host}).TotalSeconds
) | Out-Null;
# If the runtime is under 10 seconds, measure it across 19 more trials
if ($runtimes[0] -lt 10.0) {
foreach ($i in 2..20) {
Write-Progress -Activity "Measuring Performance..." `
-Status "$i of 20" `
-PercentComplete (($i/20) * 100)
$runtimes.Add(
@(Measure-Command {& python src/p43.py}).TotalSeconds
) | Out-Null;
};
$runtimes | Measure-Object -Sum -Average -Maximum -Minimum;
}
# If it's over 10 seconds, just print out the runtime from the first trial
else {
Write-Host "$($runtimes[0]) seconds"
}
PS > .\measure_performance.ps1
Bruteforce CPU
Correct solution!
583.0698225 seconds
Our first solution completes in a little under 10 minutes. Not terrible, but not anywhere near good either. There is clearly a lot of room for improvement. But before we go massively parallel with a GPU, let’s see how much our performance improves with CPU-based parallelism.
Parallel CPU #
Python provides a very convenient way to implement parallel programming. Using the Pool class in the multiprocessing library, we can simply use map() with a function and an iterable object. Pool.map() will automatically organize a pool of worker processes and execute the solution in parallel, mapping one function call for each element in the iterable. If you’re familiar with functional programming paradigms, this will be an easy concept to grasp. Our first multiprocessing version of the solution looks like this:
# Function for Map
def is_pandigital_and_substring_divisible(n):
# If this number passes both tests, include it in the final sum
return n if is_pandigital(n) and is_substring_divisible(n) else 0
def bruteforce_multiprocessed() -> List[int]:
# Create a process pool context using the default number of workers
with multiprocessing.Pool() as pool:
# Apply the function in-parallel to the entire problem space
res = pool.map( is_pandigital_and_substring_divisible,
range(0, 10_000_000_000, 9) )
# The sum of all valid numbers is the solution
return sum(res)
When we run this solution, we see that it completes in a little over 4 minutes. So, about a 2x improvement over the single-threaded solution.
PS > .\measure_performance.ps1
Bruteforce CPU - Multiprocessed
Correct solution!
251.7919883 seconds
However, it’s kind of strange to only get a 2x speed-up when we’re using 6x as many cores. This means we’re probably wasting a lot of time with multiprocessing overhead. Let’s try to fix this and optimize our CPU solution a bit further before moving on to GPUs.
Parallel CPU v2 #
We’ll do one last optimization by refactoring the work into a few large functions, instead of many smaller ones. Rather than one call for every number in the search space, we’ll divide up the entire search space into six large chunks and assign a worker to each chunk.
import multiprocessing
def bruteforce_chunk(iter) -> int:
solution = 0
for n in iter:
if is_pandigital(n) and is_substring_divisible(n):
solution += n
return solution
def bruteforce_multiprocessed_v2() -> int:
# Partition the search space into N chunks,
# where N is how many CPU cores we have.
search_space = range(0, 10_000_000_000, 9)
cores = multiprocessing.cpu_count()
size = len(search_space) // cores
search_space_chunks = [search_space[i*size:(i+1)*size] for i in range(cores)]
# Set the number of workers equal to the number of CPU cores
with multiprocessing.Pool(processes=cores) as pool:
# Execute one function call against each chunk, in-parallel
res = pool.map(bruteforce_chunk, search_space_chunks)
solution = sum(res)
return solution
This implementation completes in a little under 2 minutes. So, about a 5x improvement over the single-threaded solution. This is a lot closer to our expectations, but still well over Project Euler’s “one-minute rule”.
PS > .\measure_performance.ps1
Bruteforce CPU - Multiprocessed
Correct solution!
112.6452161 seconds
This is probably about as close as we can get with just raw CPU power, aside from actually solving the problem as intended or getting a better CPU. I think it’s finally time to show what we can do with GPUs.
Introduction to OpenCL #
To get a proper overview of OpenCL, I highly recommend the Hands On OpenCL course I mentioned at the beginning. But in the meantime, I’ll give you a quick overview to get us started, somewhat paraphrased from Khronos Group’s OpenCL Guide.
In the OpenCL platform model, a host connects to one or more compute devices. A host describes the end device that sets up the OpenCL environment and manages the work. This is usually your main CPU. Compute devices are physical hardware, such as GPUs, that can execute OpenCL commands. Each device contains many compute units that, in turn, contain many processing elements. A processing element is an individual “core” that executes OpenCL code. The host accesses these devices through an OpenCL platform, which describes a vendor’s specific OpenCL driver. To interact with these devices, the host combines one or more compute devices into an OpenCL context. However, these devices must be within the same platform.4
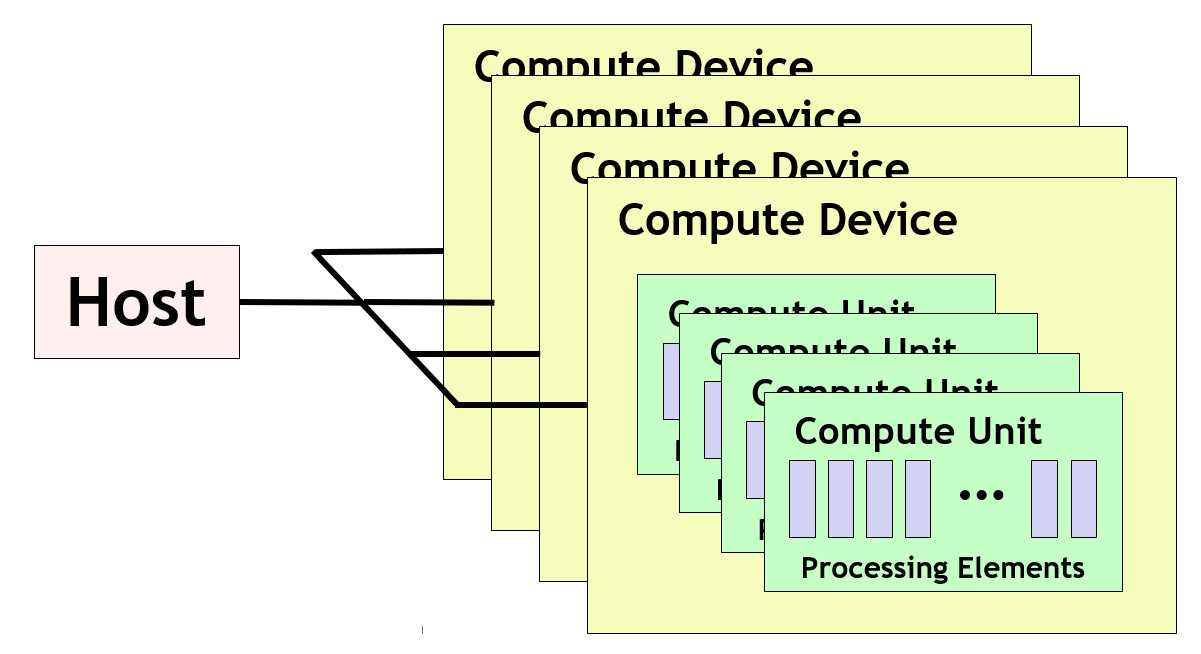
While GPUs are the most likely type of device because of their sheer ubiquity, you can compile your OpenCL programs for other types of devices. For example, Xilinx’s Vitis platform allows you to use OpenCL on some of their FPGA devices. You can also use OpenCL on CPUs, such as with Intel’s OpenCL CPU runtime. This may seem counter-intuitive, but CPUs are just better at some types of problems. Such as a small number of heavy tasks or tasks with a lot of control-flow branching. It can also be a valuable way to debug an OpenCL program since you can step-by-step debug on a CPU. This type of debugging isn’t currently possible when running on a GPU.
Now, let’s talk about how OpenCL does work. OpenCL is designed around kernel functions, which are considered its basic unit of executable code.5 To conceptualize this, let’s first look at how we would normally work on a range of memory—with a for loop. For example, if we wanted to multiply all integers in a list by 5, it would look like this:
for i in range(len(values)):
values[i] *= 5
OpenCL achieves this same result by invoking a kernel against each item in parallel. OpenCL creates one work-item (or thread) for each object in the list and every work-item runs the kernel at the same time. This is a very similar concept to a map in functional programming. That same for loop will look like this in OpenCL C:
__kernel void multiply_by_five(
__global const int *value,
__global const int *result)
{
size_t i = get_global_id(0);
result[i] = value[i] * 5;
}
Let’s dig into what each of these parts mean. The __kernel keyword is a function qualifier.6 As you can guess, this keyword is what identifies the function as a kernel function. The key difference between a kernel function and a non-kernel function is that the host can call a kernel function. On the other hand, non-kernel functions can only be called from within the device itself. You create a non-kernel function by simply not adding the __kernel keyword.
The __global keyword is known as an address space qualifier. There are four such qualifiers, __global, __local, __constant, and __private, one for each type of device memory.7 Global and constant memory is visible to all work-items, while private memory is only accessible to the work-item that created it. It’s also important to note that variables not given an address space qualifier will normally be put into private memory, by default.8 (such as size_t i, where i is saved into private memory) We won’t use local memory in this section, but just make a note that it is shared between all work-items within a work-group. We will make use of work-groups near the end when we discuss how to synchronize work-items to collaborate on a single result during execution. In summary, global/constant memory is accessible to all, private memory is accessible to only one, and local memory is accessible to some.
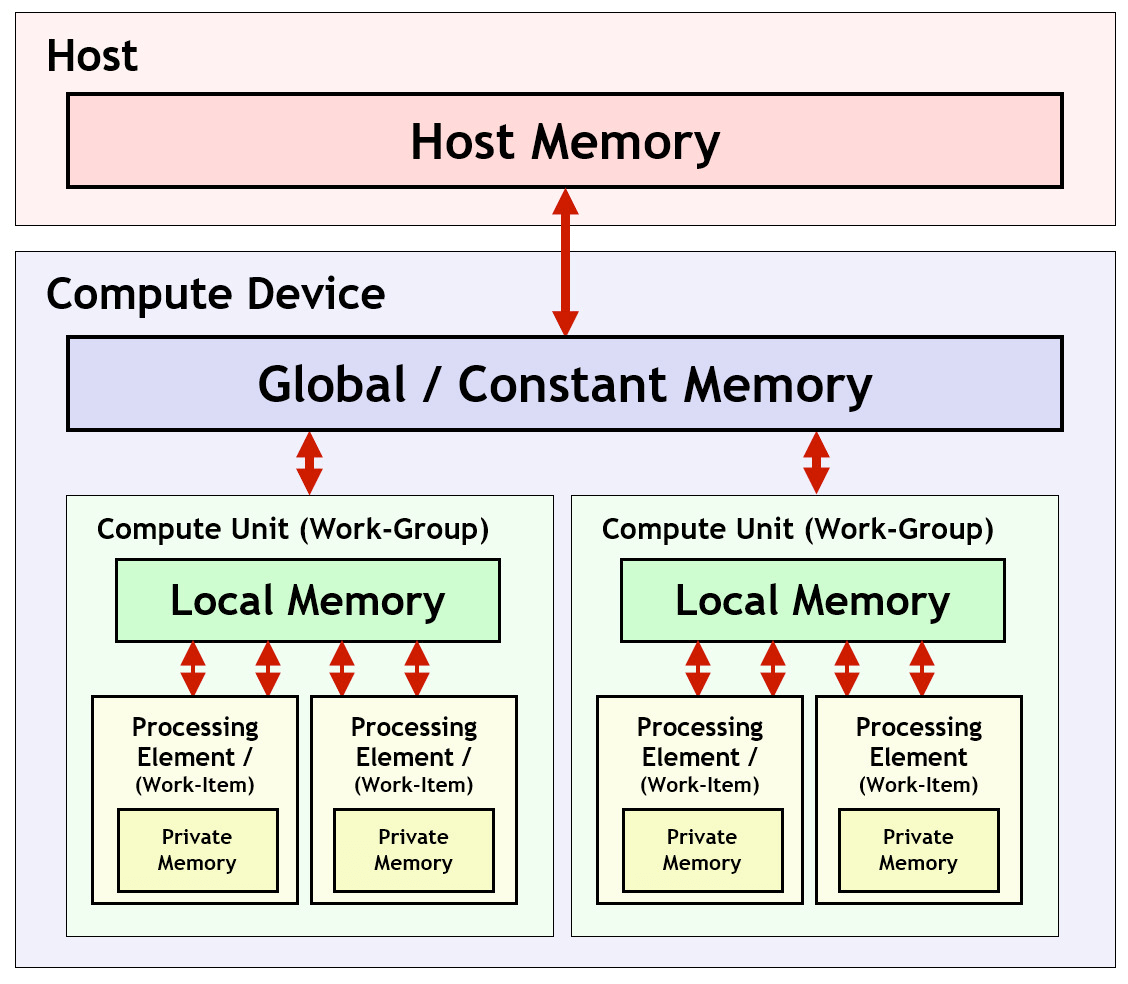
get_global_id(0) is a built-in function that provides the work-item’s global ID.9 When you run the kernel, you specify how many work-items to create. All of those N work-items are numbered from 0 to N-1. This is what allows the kernel to run against each item in the array, even though we’re running the same code for all work-items. Work-item 0 operates on value[0], work-item 1 operates on value[1], and so on.
The 0 parameter in get_global_id(0) simply refers to the dimension we want to retrieve.9 Since we’re looking at a 1D-array, we only have to worry about one dimension, 0. If we were working on a 2D-array, (such as an image) we would need to determine the work-item’s X and Y position by x = get_global_id(0) and y = get_global_id(1).
The final line (result[i] = value[i] * 5) is how we return our results to the host from the device. Because we can’t simply use a return keyword to send data from the device to the host, we have to store our results into an output buffer that the host reads after the kernel finishes running.
These kernels and other helper functions are collected into a single OpenCL program. To initiate work, the host uses an OpenCL command queue to load kernels and transfer data into a device.5 During execution, the OpenCL loads a kernel onto the device and runs them in parallel across many processing elements. By running many many copies of the kernel in parallel, OpenCL can achieve massive boosts in performance over regular CPU-based programs.
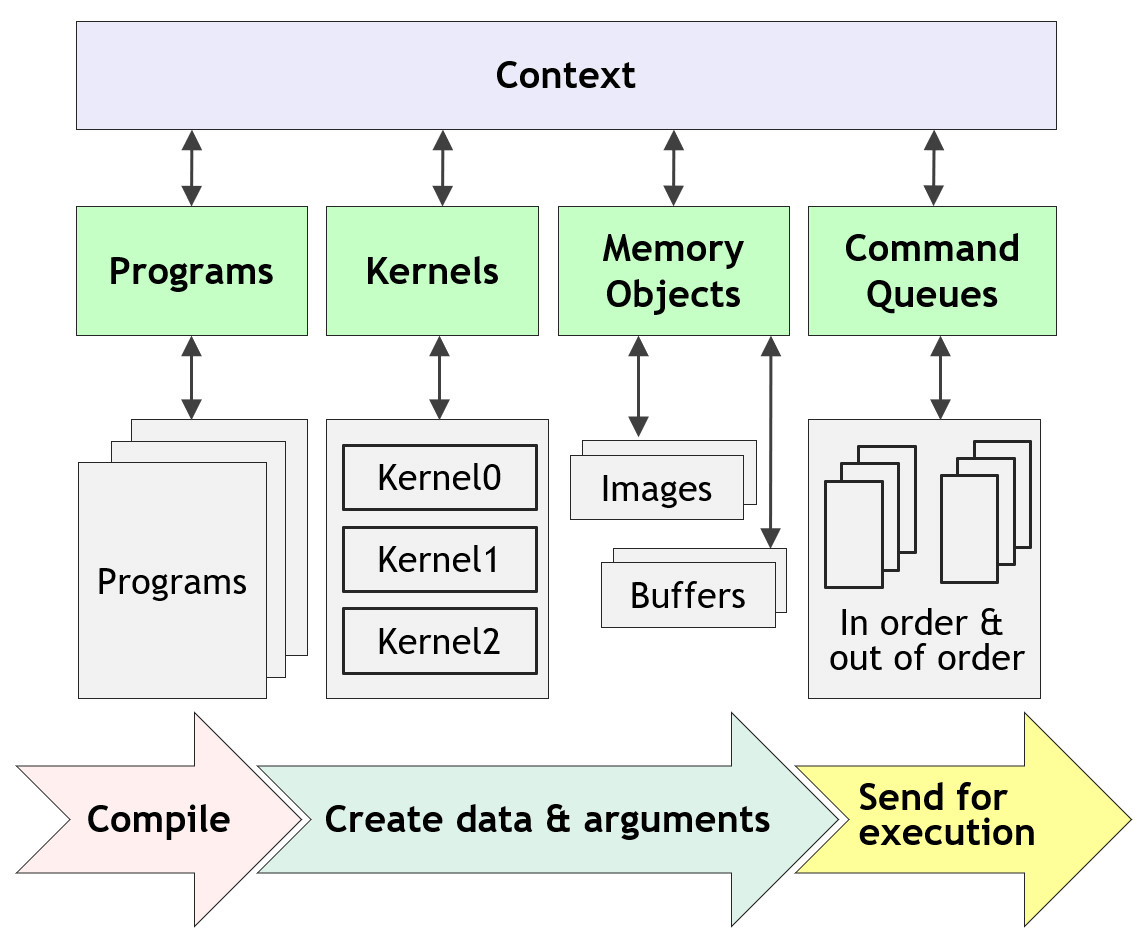
PyOpenCL will let us abstract away some of these concepts, but we do still require a good amount of boilerplate code. At a minimum, we will need to create:
- A context for the platform and devices we’re using.
- A command queue for the specific device we want to use.
- The kernel we want to run on the device.
- Memory buffers for the data we want to compute and receive.
Level 1: Functional OpenCL - GPU Computation as Simply as Possible #
If you just want to get a solution quickly and without too much headache, PyOpenCL provides several pre-designed kernels10 that’ll likely match your use case. Many of these will also be very familiar to functional programmers. But first, let’s think of Problem 43 in functional programming terms. From this perspective, our solution strategy looks like this:
- Range: For all integers that are multiples of 9 and less than 10,000,000,000…
- Filter: Filter out all integers that are not:
- Pandigital
- And substring divisible
- Reduce: Return the sum of all remaining integers.
If you wrote this in a functional language like Clojure, it would look something like this:
(->> (range 0 10000000000 9)
(filter is-pandigital?)
(filter is-substring-divisible?)
(reduce +))
The good news is that PyOpenCL has pre-designed kernels for filtering and reduction. The bad news is that we can’t combine them as elegantly as we can in a normal functional language. It’s either we apply a filter against the range, or we apply a reduction. Thankfully, we can still complete the task with either method. Let’s start with PyOpenCL’s version of filter, copy_if.
Solve using a Filter: copy_if #
Our strategy for this method is that not everything needs to be on the GPU. As we know from the previous solutions, there will only be a handful of numbers that satisfy both predicates. If the GPU can give us just those numbers, then it’s trivial to finish the calculation on the host.
First, let’s get the boilerplate code out of the way. With the pre-designed kernels, we only need to define the context and provide a command queue.
import pyopencl as cl
def bruteforce_gpu_filter() -> np.int64:
context = cl.create_some_context(interactive=False)
queue = cl.CommandQueue(context)
The create_some_context() function is the quick and dirty way of defining an OpenCL context. When you run it with the default parameters, it’ll pause the host program to ask you which platform and device to use. Setting interactive=False has it figure out the platform and device on its own. Similarly, the CommandQueue() constructor also figures out the device on its own if you don’t explicitly specify it. For most general users with a single GPU, those options should suffice. Now we can get into the actual computation part of the problem. The documentation for copy_if11 lets us know what we need to do next.
We first need to define the input buffer, ary. This will be the data that copy_if is filtering. As you can guess, Python’s data types don’t mesh well with C’s. A Python int could be anything from a C int, long, long long, or a completely unpresentable value. To avoid such issues, we can declare our buffers using the Numpy library, which lets us specify an explicit data type. Since all of our input values are expected to be 10-digit numbers, we will need to use 64-bit integers to represent them. (Numpy: int64 -> C: long) After we declare the array, we can transfer it to the device using PyOpenCL’s array.to_device() function. This function does two things: sends the data to the device and provides us with an OpenCL array that represents the on-device memory. Using OpenCL arrays slightly simplifies the memory buffer allocation process and is a little easier to work with than raw buffers. To avoid confusion, it’s also a good habit to mark which objects exist on the host (ary_host) and which objects exist on the device. (ary_dev)
import pyopencl as cl
import numpy as np
def bruteforce_gpu_filter() -> np.int64:
context = cl.create_some_context(interactive=False)
queue = cl.CommandQueue(context)
ary_host = np.arange(0, 10_000_000_000, 9, dtype=np.int64)
ary_dev = cl.array.to_device(queue, ary_host)
Now we need to define the predicate functions: is_pandigital and is_substring_divisible. We have a slight problem though, the filter argument for copy_if expects a single C expression, but we need to perform two relatively complex operations. Thankfully, we can declare a preamble and include those two predicates as helper functions. This will allow us to use "is_pandigital(ary[i]) && is_substring_divisible(ary[i])" as the filter argument. Designing these functions in OpenCL C requires a different approach from Python, but there still is some overlap.
Let’s start with the is_pandigital function. Our first pothole is that OpenCL C does not have a set() object like Python. So our previous method of adding each digit to the set and checking for it later won’t work. However, we can mimic its behavior using a bitmask.
bool is_pandigital(long x) {
// A mask with the last 10-bits set,
// corresponding to the digits 9 thru 0
uint set = 0b1111111111;
for (size_t i = 0; i < 10; ++i) {
// Take the least-significant, base-10 digit...
uint digit = x % 10;
// Shift x to the right by one base-10 digit...
x /= 10;
// And toggle the corresponding bit in the mask
set ^= (1 << digit);
}
// If we see all 10 digits only once, all bits will be set to 0.
// If we don't see a digit or see a digit twice, at least
// one bit will be set to 1, making the mask non-zero.
return set == 0;
}
And now the is_substring_divisible function. Although this one is more straightforward, we do have to pre-compute the powers of ten since OpenCL C doesn’t provide an integer power function. Well… there’s a pow() function alright. But, it only accepts float values. On the bright side, these pre-computed values are a great candidate to put into __constant memory space.
__constant long divisor[7] = {2, 3, 5, 7, 11, 13, 17};
__constant long pow10[10] = {
1, 10, 100, 1000, 10000, 100000,
1000000, 10000000, 100000000, 1000000000
};
bool is_substring_divisible(const long x) {
// Loop through the 7 possible substrings
for (size_t i = 0; i < 7; ++i) {
// A sliding window of 3 digits, starting from the 2nd digit
const long substring = (x % pow10[9-i]) / pow10[6-i];
// Predicate fails if any substring is not divisible by its respective divisor
if (substring % divisor[i] != 0)
return false;
}
// Predicate succeeds if all substrings pass
return true;
}
Finally, let’s combine all of that and see how fast it runs! One thing to note is that copy_if appears to do some string formatting on the backend, so we have to escape our % chars by doubling them up.
import pyopencl as cl
import numpy as np
def bruteforce_gpu_filter() -> np.int64:
context = cl.create_some_context(interactive=False)
queue = cl.CommandQueue(context)
ary_host = np.arange(0, 10_000_000_000, 9, dtype=np.int64)
ary_dev = cl.array.to_device(queue, ary_host)
result, count, event = cl.algorithm.copy_if(ary_dev,
"is_pandigital(ary[i]) && is_substring_divisible(ary[i])",
preamble="""
__constant long divisor[7] = {2, 3, 5, 7, 11, 13, 17};
__constant long pow10[10] = {
1, 10, 100, 1000, 10000, 100000,
1000000, 10000000, 100000000, 1000000000
};
bool is_substring_divisible(const long x) {
for (size_t i = 0; i < 7; ++i) {
const long substring = (x %% pow10[9-i]) / pow10[6-i];
if (substring %% divisor[i] != 0)
return false;
}
return true;
}
bool is_pandigital(long x) {
uint set = 0b1111111111;
for (size_t i = 0; i < 10; ++i) {
uint digit = x %% 10;
x /= 10;
set ^= (1 << digit);
}
return set == 0;
}
""")
# copy_if returns both a result and count value. We can't just use
# result directly because it's the *entire* output buffer.
# copy_if just "front loads" the matching results and provides us
# a count how many matches it found.
# To get only the matching values, we need to take only the
# first few elements, according to the count value.
solutions = []
for r in result.get()[:count.get()]:
solutions.append(r)
return sum(solutions)
It should run perfectly the very first time we try it out, right?
PS > python3 .\src\p43.py
Bruteforce GPU - Filter Kernel (copy_if)
Traceback (most recent call last):
File "C:\█████████\project-euler\src\p43.py", line 156, in <module>
main()
File "C:\█████████\pproject-euler\src\p43.py", line 137, in main
solution = sum(bruteforce_gpu_filter())
File "C:\█████████\project-euler\src\p43.py", line 96, in bruteforce_gpu_filter
n_dev = cl.array.to_device(queue, n_host)
File "C:\█████████\Python39\site-packages\pyopencl\array.py", line 2316, in to_device
result.set(ary, async_=async_, queue=queue)
File "C:\█████████\Python39\site-packages\pyopencl\array.py", line 800, in set
event1 = cl.enqueue_copy(queue or self.queue, self.base_data, ary,
File "C:\█████████\Python39\site-packages\pyopencl\__init__.py", line 1930, in enqueue_copy
return _cl._enqueue_write_buffer(queue, dest, src, **kwargs)
pyopencl._cl.MemoryError: clEnqueueWriteBuffer failed: MEM_OBJECT_ALLOCATION_FAILURE
Oops… well, we’re trying to allocate around 1.1 billion 64-bit integers, which take up 8 bytes each. \(1,111,111,111 \text{ long integers} \times 8 \text{ bytes per integer} \approx 8477 \text{ MB}\). My RTX 3070 only has around 8 GB of memory and limits the max allocation size to around 2048 MB.
The solution is pretty simple, we just need to divide our total search space into several smaller chunks and then combine the results as we go. To keep things consistent, we’re going to set the chunk size to \(32^4\) for all of our remaining solutions.
def bruteforce_gpu_filter(chunk_size: np.int64=32**4) -> np.int64:
context = cl.create_some_context(interactive=False)
queue = cl.CommandQueue(context)
solutions = []
chunk_range = chunk_size * 9
for ary_base in range(0, 10_000_000_000, chunk_range):
ary_host = np.arange(ary_base, ary_base + chunk_range, 9, dtype=np.int64)
ary_dev = cl.array.to_device(queue, ary_host)
result, count, event = cl.algorithm.copy_if(n_dev,
"is_pandigital(ary[i]) && is_substring_divisible(ary[i])",
preamble= """
__constant long divisor[7] = {2, 3, 5, 7, 11, 13, 17};
__constant long pow10[10] = {
1, 10, 100, 1000, 10000, 100000,
1000000, 10000000, 100000000, 1000000000
};
bool is_substring_divisible(const long x) {
for (size_t i = 0; i < 7; ++i) {
const long substring = (x %% pow10[9-i]) / pow10[6-i];
if (substring %% divisor[i] != 0)
return false;
}
return true;
}
bool is_pandigital(long x) {
uint set = 0b1111111111;
for (size_t i = 0; i < 10; ++i) {
uint digit = x %% 10;
x /= 10;
set ^= (1 << digit);
}
return set == 0;
}
""")
for r in result.get()[:count.get()]:
solutions.append(r)
return sum(solutions)
PS C:\Users\berna\OneDrive\Projects\Python\project-euler> .\measure_performance.ps1
Bruteforce GPU - Filter Kernel (copy_if)
Correct solution!
Count : 20
Average : 8.35425489
Sum : 167.0850978
Maximum : 9.2128908
Minimum : 7.828059
Property :
Our first attempt at GPU computation significantly reduces the total runtime to just over 8 seconds! Around a 72x improvement over the original solution, 14x over the CPU multiprocessed one, and well under Project Euler’s “one-minute rule”. Now let’s see how to solve this using a reduction.
Solve using a Reduction: ReductionKernel #
There are two ways we can solve this using a reduce expression. The first way is to perform filtering during the reduction operation. For the expression a + b, where b is the next value, we can check if b satisfies both predicates. If it fails either one, then we don’t include it in the total sum by setting it to 0.
The second way is to perform that pseudo-filtering before the reduction. I know I said before that we can’t combine functions like in other languages. However, PyOpenCL’s ReductionKernel12 allows you to specify a map_expr in addition to the reduce_expr. We can perform a pseudo-filter by testing all values with the map operation and setting them to 0 if they fail either predicate. That way, any “invalid numbers” won’t be included in the final sum. Although we’re asking the GPU to waste a lot of time adding up zeroes, it’s still surprisingly quick.
Let’s replace our filter kernel with a reduction kernel and see how it fast runs. It’s also good to note that ReductionKernel is managed differently from copy_if. Here, you initialize the kernel first and then run it against data. Compared to copy_if where you’re building and executing the kernel in the same call. ReductionKernel also does not appear to be doing string formatting on the backend. So we need to leave the % characters as-is.
def bruteforce_gpu_reduce(chunk_size: np.int64=32**4) -> np.int64:
context = cl.create_some_context(interactive=False)
queue = cl.CommandQueue(context)
kernel = cl.reduction.ReductionKernel(
context,
np.int64,
0,
"a + b",
"is_pandigital(x[i]) && is_substring_divisible(x[i]) ? x[i] : 0",
"__global long *x",
preamble="""
__constant long divisor[7] = {2, 3, 5, 7, 11, 13, 17};
__constant long pow10[10] = {
1, 10, 100, 1000, 10000, 100000,
1000000, 10000000, 100000000, 1000000000
};
bool is_substring_divisible(const long x) {
for (size_t i = 0; i < 7; ++i) {
const long substring = (x % pow10[9-i]) / pow10[6-i];
if (substring % divisor[i] != 0)
return false;
}
return true;
}
bool is_pandigital(long x) {
uint set = 0b1111111111;
for (size_t i = 0; i < 10; ++i) {
uint digit = x % 10;
x /= 10;
set ^= (1 << digit);
}
return set == 0;
}
""")
chunk_range = chunk_size * 9
solution = np.int64(0)
for ary_base in range(0, 10_000_000_000, chunk_range):
ary_host = np.arange(ary_base, ary_base + chunk_range, 9, dtype=np.int64)
ary_dev = cl.array.to_device(queue, ary_host)
result = kernel(ary_dev).get()
solution += np.int64(result)
return solution
PS > .\measure_performance.ps1
Bruteforce GPU - Elementwise Reduce Kernel
Correct solution!
Count : 20
Average : 5.04815725
Sum : 100.963145
Maximum : 6.252973
Minimum : 4.7605684
Property :
A slight improvement over the filter kernel with a runtime at a little over 5 seconds. About a 110x improvement over the original solution and 25x over the multiprocessed one. With even bare minimum effort, we’ve already seen close to optimal gains from GPU computation. But now let’s put the pre-made kernels behind and try to design our own.
Level 2: Making your own kernel #
The good news is that we can still use our helper functions from the previous section. All we have to do is create the kernel function. For our first attempt, let’s design the kernel using the same method as our multiprocessing solution. For each number in the search space, determine if it’s both pandigital and substring divisible. If it fails either condition, set its result to 0. Afterward, take the sum of every result to calculate the solution. Since invalid numbers are set to 0, they will not be included in the final sum.
Using our previous helper functions, the kernel function becomes very simple to implement in OpenCL C:
__kernel void valid_solutions(
__global long *n,
__global long *result)
{
size_t gid = get_global_id(0);
// If this number passes both tests, include it in the sum
if (is_pandigital(n[gid]) && is_substring_divisible(n[gid]))
result[gid] = n[gid];
// If this number fails either test, ignore it
else
result[gid] = 0;
}
The entire kernel source code, with helper functions, looks like this:
__constant long divisor[7] = {2, 3, 5, 7, 11, 13, 17};
__constant long pow10[10] = {
1, 10, 100, 1000, 10000, 100000,
1000000, 10000000, 100000000, 1000000000
};
bool is_substring_divisible(const long x) {
for (size_t i = 0; i < 7; ++i) {
const long substring = (x % pow10[9-i]) / pow10[6-i];
if (substring % divisor[i] != 0)
return false;
}
return true;
}
bool is_pandigital(long x) {
uint set = 0b1111111111;
for (size_t i = 0; i < 10; ++i) {
uint digit = x % 10;
x /= 10;
set ^= (1 << digit);
}
return set == 0;
}
__kernel void valid_solutions(
__global long *n,
__global long *result)
{
size_t gid = get_global_id(0);
if (is_pandigital(n[gid]) && is_substring_divisible(n[gid]))
result[gid] = n[gid];
else
result[gid] = 0;
}
Our next step is to create the host function that will call this kernel. The overall process is similar to the pre-built kernels. We just have to manually specify some additional parameters.
def bruteforce_gpu_custom(chunk_size: np.int64=32**4) -> np.int64:
context = cl.create_some_context(interactive=False)
queue = cl.CommandQueue(context)
# We have to provide the entire OpenCL source code and build it into an OpenCL program
program = cl.Program(context, open('src/opencl/p43_bruteforce_naive.cl').read()).build()
# Then we reference the desired kernel function to run it later
kernel = program.valid_solutions
chunk_range = chunk_size * 9
solution = 0
for n_base in range(0, 10_000_000_000, chunk_range):
n_host = np.arange(n_base, n_base + chunk_range, 9, dtype=np.int64)
n_dev = cl.array.to_device(queue, n_host)
# In addition to the input arrays, we also have to define the results array
# and provide it to the kernel
result_dev = cl.array.empty(queue, n_host.shape, dtype=np.int64)
# When executing a custom kernel, we have to specify:
# 1. Global Size - The total number of work-items, globally. (n_dev.shape)
# 2. Local Size - The number of items within each work-group. (None)
# - `None` technically means, use an implementation-defined local size. But
# for our case, it means "we don't care about the local size".
# 3. The parameters for the kernel function. (n_dev.data, result_dev.data)
# - Custom kernels require memory buffers, not OpenCL arrays. But,
# we can just retrieve the underlying buffer object for
# an array using the `.data` field.
kernel(queue, n_dev.shape, None, n_dev.data, result_dev.data)
# Just as how we needed to define the results array, we also need to manually
# retrieve the results from the device after the kernel finishes.
result_host = result_dev.get()
solution += sum(result_host)
return solution
Now we’ve implemented our first custom kernel! Let’s measure the total runtime and see how much of an improvement we get.
PS > .\measure_performance.ps1
Bruteforce GPU - Custom-built Kernel
Correct solution!
56.8248093 seconds
If you just compare it to the CPU-based solutions, that’s not too bad. It’s about 10x better than the single-threaded solution and almost 2x better than the optimized multi-processing solution. Most importantly, it’s (very) technically under Project Euler’s one-minute rule! However, it’s still significantly worse than the pre-built kernels. Let’s run the host function through line_profiler and see what’s slowing us down.
PS > kernprof -vl .\src\p43_post.py
Bruteforce GPU - Custom-built Kernel
Correct solution!
Wrote profile results to p43_post.py.lprof
Timer unit: 1e-06 s
Total time: 56.2973 s
File: .\src\p43_post.py
Function: bruteforce_gpu_custom at line 149
Line # Hits Time Per Hit % Time Line Contents
==============================================================
149 @profile
150 def bruteforce_gpu_custom(chunk_size: np.int64=32**4) -> np.int64:
151 1 200173.6 200173.6 0.4 context = cl.create_some_context(interactive=False)
152
153 1 54.6 54.6 0.0 queue = cl.CommandQueue(context)
154 1 66632.5 66632.5 0.1 program = cl.Program(context, open('src/opencl/p43_bruteforce_naive.cl').read()).build()
155 1 18281.1 18281.1 0.0 kernel = program.valid_solutions
156
157 1 1.4 1.4 0.0 chunk_range = chunk_size * 9
158 1 0.4 0.4 0.0 solution = 0
159 35 134.9 3.9 0.0 for n_base in range(0, 10_000_000_000, chunk_range):
160 34 1422576.7 41840.5 2.5 n_host = np.arange(n_base, n_base + chunk_range, 9, dtype=np.int64)
161 34 2605552.6 76633.9 4.6 n_dev = cl.array.to_device(queue, n_host)
162 34 65208.4 1917.9 0.1 result_dev = cl.array.empty(queue, n_host.shape, dtype=np.int64)
163
164 34 17532.6 515.7 0.0 kernel(queue, n_dev.shape, None, n_dev.data, result_dev.data)
165
166 34 3679422.0 108218.3 6.5 result_host = result_dev.get()
167 34 48221722.7 1418286.0 85.7 solution += sum(result_host)
168
169 1 0.5 0.5 0.0 return solution
The clear culprit by an overwhelming margin is the line solution += sum(result_host), taking up 85.7% of the total runtime. This makes sense. We’re offloading the more computationally expensive part of the operation to the GPU, which is testing if an element passes both predicates. But, we’re still asking the CPU to add up over 1 billion elements. That’s a big ask, even if they’re simple add operations. If we can also offload the sum operation to the GPU, we should see a significant improvement. By a much smaller margin, we also see that we’re spending a lot of time both creating data on the host and transferring data with the device, about 13.7% of the total runtime. This would be a solid candidate for a second optimization after we implement the GPU sum.
Level 3: Optimizing your custom kernel #
The Naive Sum #
We’ve been working with the assumption that each work-item is independent of the other and only corresponds to one element in the problem space. Exactly like a map operation. However, a sum operation will require a work-item to operate on multiple different elements. So, how can we perform a sum operation on the GPU?
Well, when we execute the kernel function, we’re not saying “run a work-item against each element in our input array.” We’re actually saying, “spawn N number of work-items and run the kernel function on each one.” So, the work-item to element relationship doesn’t have to be one-to-one. It can be one-to-many, which is what’s necessary for our sum operation.
Let’s make a first attempt at the problem in a way that’s completely not best practice. As far as we know, our work-items can’t work together to compute a single sum. But, we can compute many partial sums to at least significantly reduce the number of values the host has to add up. We’re going to take a two-stage approach:
- Perform the mapping operation using the previous kernel.
- Run another kernel that reduces the results to a few partial sums.
The overall concept of the sum kernel is pretty simple. We just need to logically divide up the results into N equally-sized chunks. And then we spawn N work-items that sum up every value in their assigned chunk. To accomplish this within the kernel, we will need to use a scalar argument. Using scalar arguments is actually very easy, both on the host and device sides. The sum kernel looks like this:
__kernel void sum_results(
// Scalar argument for the chunk size
const int chunk_size,
__global long *input,
__global long *partial_sum)
{
size_t gid = get_global_id(0);
// The base index for this work-item's assigned chunk
size_t chunk_id = gid * chunk_size;
// Add up all elements in its assigned chunk and save the
// result in the partial_sum buffer
partial_sum[gid] = 0;
for (size_t i = 0; i < chunk_size; ++i)
partial_sum[gid] += input[chunk_id + i];
}
Now, let’s integrate this extra kernel function into our previous host program and see how much better it runs.
def bruteforce_gpu_custom_sum_naive(chunk_size: np.int64=32**4, num_of_sum_threads: np.int32=1024) -> np.int64:
# We MUST be able to equally-divide up the search space across each sum work-item.
# Otherwise, we might double-count some elements or access out-of-bounds.
assert chunk_size % num_of_sum_threads == 0
# This will be our `chunk_size` argument.
# Passing a scalar argument is even simpler than passing arrays,
# you just directly provide a variable that matches the scalar's data-type.
sum_chunk_size = np.int32(chunk_size // num_of_sum_threads)
context = cl.create_some_context(interactive=False)
queue = cl.CommandQueue(context)
program = cl.Program(context, open('src/opencl/p43_bruteforce_naive.cl').read()).build()
# Since we're calling two separate kernels, we create two separate references
valid_solutions_kernel = program.valid_solutions
sum_results_kernel = program.sum_results
chunk_range = chunk_size * 9
solution = 0
for n_base in range(0, 10_000_000_000, chunk_range):
# Stage 1 - Perform the Mapping Operation
n_host = np.arange(n_base, n_base + chunk_range, 9, dtype=np.int64)
n_dev = cl.array.to_device(queue, n_host)
result_dev = cl.array.empty(queue, n_host.shape, dtype=np.int64)
valid_solutions_kernel(queue, n_dev.shape, None, n_dev.data, result_dev.data)
# Stage 2 - Partially Reduce the Results
sum_dev = cl.array.empty(queue, num_of_sum_threads, dtype=np.int64)
sum_results_kernel(queue, sum_dev.shape, None, sum_chunk_size, result_dev.data, sum_dev.data)
sum_host = sum_dev.get()
# Compute the total sum on the host
solution += sum(sum_host)
return solution
PS > .\measure_performance.ps1
Bruteforce GPU - Custom-built Sum Kernel (Naive)
Correct solution!
Count : 20
Average : 5.681275685
Sum : 113.6255137
Maximum : 6.3775643
Minimum : 5.4233037
Property :
That’s shockingly good! We beat the copy_if kernel and are getting close to the performance of the reduction kernel. Let’s see what’s still slowing us down.
PS > kernprof -vl .\src\p43_post.py
Bruteforce GPU - Custom-built Sum Kernel (Naive)
Correct solution!
Wrote profile results to p43_post.py.lprof
Timer unit: 1e-06 s
Total time: 5.53483 s
File: .\src\p43_post.py
Function: bruteforce_gpu_custom_sum_naive at line 170
Line # Hits Time Per Hit % Time Line Contents
==============================================================
170 @profile
171 def bruteforce_gpu_custom_sum_naive(chunk_size: np.int64=32**4, sum_threads: np.int32=1024) -> np.int64:
172 1 1.8 1.8 0.0 assert chunk_size % sum_threads == 0
173 1 221.6 221.6 0.0 sum_chunk_size = np.int32(chunk_size // sum_threads)
174
175 1 133339.7 133339.7 2.4 context = cl.create_some_context(interactive=False)
176
177 1 39.4 39.4 0.0 queue = cl.CommandQueue(context)
178 1 6902.6 6902.6 0.1 program = cl.Program(context, open('src/opencl/p43_bruteforce_naive.cl').read()).build()
179
180 1 3236.0 3236.0 0.1 valid_solutions_kernel = program.valid_solutions
181 1 617.1 617.1 0.0 sum_results_kernel = program.sum_results
182
183 1 1.1 1.1 0.0 chunk_range = chunk_size * 9
184 1 0.4 0.4 0.0 solution = 0
185 1061 1282.3 1.2 0.0 for n_base in range(0, 10_000_000_000, chunk_range):
186 1060 1741004.3 1642.5 31.5 n_host = np.arange(n_base, n_base + chunk_range, 9, dtype=np.int64)
187 1060 2159472.2 2037.2 39.0 n_dev = cl.array.to_device(queue, n_host)
188 1060 220299.4 207.8 4.0 result_dev = cl.array.empty(queue, n_host.shape, dtype=np.int64)
189 1060 114762.9 108.3 2.1 valid_solutions_kernel(queue, n_dev.shape, None, n_dev.data, result_dev.data)
190
191 1060 556824.7 525.3 10.1 sum_dev = cl.array.empty(queue, sum_threads, dtype=np.int64)
192 1060 143803.2 135.7 2.6 sum_results_kernel(queue, sum_dev.shape, None, sum_chunk_size, result_dev.data, sum_dev.data)
193 1060 399882.8 377.2 7.2 sum_host = sum_dev.get()
194
195 1060 53138.0 50.1 1.0 solution += sum(sum_host)
196
197 1 0.4 0.4 0.0 return solution
At 91.6% of the total runtime, the time spent passing data between the device is now the biggest culprit. Having to run a second kernel also isn’t helping things. To optimize things further, let’s see how we can put both stages of our solution into one kernel.
Summing with Work-Groups #
We designed the previous sum kernel with the assumption that work-items cannot collaborate. On a global scale, this is true. We cannot reliably have all work-items collaborate towards a single solution. However, we can divide up all of our work-items into equally-sized work-groups. Those work-items in a work-group can collaborate towards a single solution. The reason they can is because of three important abilities:
- Each work-item in the work-group is assigned a local ID. Like with the global ID we’ve been using, this is what allows us to assign different tasks within the work-group.
- We can assign local memory to each work-group. This memory is much quicker to access than global memory and is accessible to all members of the work-group.
- We can synchronize execution within a work-group using the
barrier(CLK_LOCAL_MEM_FENCE)function. When a work-item reaches abarriercall during execution, it must wait until all other work-items in the work-group also reach this samebarrierbefore continuing. The flagCLK_LOCAL_MEM_FENCEjust means to also wait until all changes to local memory are completed. This allows us to avoid race conditions between each work-item.
To give a simple demonstration of how this all might work, let’s start by combining both our kernels into one.
__kernel void sum_of_valid_solutions(
__global long *n,
__local long *result, // Local memory that the work-group will collaborate on
__global long *sum)
{
size_t gid = get_global_id(0); // This work-item's global ID. Maps to an index in `n`.
size_t lid = get_local_id(0); // This work-item's ID within the work-group. Maps to an index in `result`.
size_t wg_id = get_group_id(0); // The ID for the entire work-group. Maps to an index in `sum`.
size_t wg_size = get_local_size(0); // The number of work-items in the work-group. Does the same job as `chunk_size` in the naive sum kernel.
// Stage 1 - valid_solutions: Concurrently apply predicate against the entire problem space
if (is_pandigital(n[gid]) && is_substring_divisible(n[gid]))
result[lid] = n[gid];
else
result[lid] = 0;
// Wait until everyone finishes the map operation
barrier(CLK_LOCAL_MEM_FENCE);
// Stage 2 - sum_results: Only the first work-item in the group will sum up the result array
if (lid == 0) {
sum[wg_id] = 0;
for (size_t i = 0; i < wg_size; ++i)
sum[wg_id] += result[i];
}
}
And after we refactor the host function, it’ll look like this. Since I’m running an RTX 3070, my maximum work-group size is 1,024 work-items. Depending on your GPU, this value may vary. The important thing is to specify a work-group size that your device can handle, otherwise you might receive an error.
def bruteforce_gpu_custom_sum_naive_v2(chunk_size: np.int64=32**4, workgroup_size: np.int32=1024) -> np.int64:
# Similar limitation to our previous solution.
# The the local workgroup size MUST evenly divide
# up the global workspace size.
assert chunk_size % workgroup_size == 0
num_of_workgroups = np.int32(chunk_size // workgroup_size)
context = cl.create_some_context(interactive=False)
queue = cl.CommandQueue(context)
program = cl.Program(context, open('src/opencl/p43_bruteforce_naive.cl').read()).build()
# Back to referencing a single kernel function
kernel = program.sum_of_valid_solutions
chunk_range = chunk_size * 9
solution = 0
for n_base in range(0, 10_000_000_000, chunk_range):
n_host = np.arange(n_base, n_base + chunk_range, 9, dtype=np.int64)
n_dev = cl.array.to_device(queue, n_host)
# Note that you define local memory as a total size in *bytes*.
# For our case, we multiply by 8 because we're storing `long` integers,
# which take up 8 bytes each.
result_local = cl.LocalMemory(workgroup_size * 8)
# Size of the sum buffer is now based on the total number of workgroups.
sum_dev = cl.array.empty(queue, num_of_workgroups, dtype=np.int64)
# We now can replace `None` with a tuple for our desired local workgroup size.
# Passing local memory is the same as global memory.
kernel(queue, n_dev.shape, (workgroup_size, ), n_dev.data, result_local, sum_dev.data)
sum_host = sum_dev.get()
solution += sum(sum_host)
return solution
Running this new kernel shows a slight improvement over the previous one. This is mainly from cutting out a data transfer (result_dev vs result_local) and eliminating a kernel call. We’re now about equal to the built-in reduction kernel.
PS > .\measure_performance.ps1
Bruteforce GPU - Custom-built Sum Kernel (Naive using Work-Groups)
Correct solution!
Count : 20
Average : 5.083549005
Sum : 101.6709801
Maximum : 5.6858026
Minimum : 4.8722905
Property :
All in all, there are a lot of issues with that sum algorithm. Each work-group can have up to 1,024 work-items. However, our sum algorithm is only using one of them; a 0.1% utilization rate. A true parallel sum would have all (or most) of those work-items contributing to the solution, in at least some part. Now that we’ve laid the foundation for how to use work-groups, let’s implement a sum operation that does just this and is closer to what the industry’s best practice is.
Parallel Sum #
We’re going to implement the kernel as described in this Nvidia CUDA webinar.13 Although it’s targeted toward CUDA programmers, it’s still a great explanation of the algorithm and all of the concepts are the same. We’re going to implement Kernel 3 from the webinar, which will strike a nice balance between simplicity and efficiency.
The overall concept of the parallel sum is pretty simple. For the current number of input values, half that number of work-items will each add up two values. This will also shrink the number of input values by half. Repeat this process until there is only one remaining input value. The first work-item will store this value into output. The kernel looks like this in OpenCL C:
__kernel void sum_of_valid_solutions(
__global long *n,
__local long *result,
__global long *sum)
{
size_t gid = get_global_id(0);
size_t lid = get_local_id(0);
size_t wg_id = get_group_id(0);
size_t wg_size = get_local_size(0);
// Stage 1 - Map: Concurrently apply predicate against the entire problem space
if (is_pandigital(n[gid]) && is_substring_divisible(n[gid]))
result[lid] = n[gid];
else
result[lid] = 0;
barrier(CLK_LOCAL_MEM_FENCE);
// Stage 2 - Sum: Perform the parallel sum operation
// Adapted from CUDA guide:
// https://developer.download.nvidia.com/assets/cuda/files/reduction.pdf
for (uint stride = wg_size / 2; stride > 0; stride >>= 1) {
if (lid < stride)
result[lid] += result[lid + stride];
barrier(CLK_LOCAL_MEM_FENCE);
}
// The first work-item stores the final result into the output array.
if (lid == 0)
sum[wg_id] = result[lid];
}
And no changes to the host program, aside from the input filename.
def bruteforce_gpu_custom_sum_good(chunk_size: np.int64=32**4, workgroup_size: np.int32=1024) -> np.int64:
assert chunk_size % workgroup_size == 0
num_of_workgroups = np.int32(chunk_size // workgroup_size)
context = cl.create_some_context(interactive=False)
queue = cl.CommandQueue(context)
program = cl.Program(context, open('src/opencl/p43_bruteforce_good.cl').read()).build()
kernel = program.sum_of_valid_solutions
chunk_range = chunk_size * 9
solution = 0
for n_base in range(0, 10_000_000_000, chunk_range):
n_host = np.arange(n_base, n_base + chunk_range, 9, dtype=np.int64)
n_dev = cl.array.to_device(queue, n_host)
result_local = cl.LocalMemory(workgroup_size * 8)
sum_dev = cl.array.empty(queue, num_of_workgroups, dtype=np.int64)
kernel(queue, n_dev.shape, (workgroup_size,), n_dev.data, result_local, sum_dev.data)
sum_host = sum_dev.get()
solution += np.sum(sum_host)
return solution
When we test the new kernel, we measure a very slight improvement over the previous, inefficient kernel.
PS > .\measure_performance.ps1
Bruteforce GPU - Custom-built Sum Kernel (Parallel)
Correct solution!
Count : 20
Average : 4.9172684
Sum : 98.345368
Maximum : 5.4164774
Minimum : 4.7205961
Property :
Let’s try to optimize this solution, one more time. Profiling the host function shows that 82.5% of our time is spent creating and transferring the input values, n. It’d be a huge win if we could skip that step altogether.
> kernprof -vl .\src\p43_post.py
Bruteforce GPU - Custom-built Sum Kernel (Parallel)
Correct solution!
Wrote profile results to p43_post.py.lprof
Timer unit: 1e-06 s
Total time: 5.10637 s
File: .\src\p43_post.py
Function: bruteforce_gpu_custom_sum_v1 at line 223
Line # Hits Time Per Hit % Time Line Contents
==============================================================
223 @profile
224 def bruteforce_gpu_custom_sum_v1(chunk_size: np.int64=32**4, workgroup_size: np.int32=1024) -> np.int64:
225 1 1.7 1.7 0.0 assert chunk_size % workgroup_size == 0
226 1 9.0 9.0 0.0 num_of_workgroups = np.int32(chunk_size // workgroup_size)
227
228 1 142818.7 142818.7 2.8 context = cl.create_some_context(interactive=False)
229 1 47.8 47.8 0.0 queue = cl.CommandQueue(context)
230
231 1 6865.1 6865.1 0.1 program = cl.Program(context, open('src/opencl/p43_bruteforce_good.cl').read()).build()
232 1 3163.1 3163.1 0.1 kernel = program.sum_of_valid_solutions
233
234 1 1.1 1.1 0.0 chunk_range = chunk_size * 9
235 1 0.4 0.4 0.0 solution = 0
236 1061 1286.0 1.2 0.0 for n_base in range(0, 10_000_000_000, chunk_range):
237 1060 1701431.1 1605.1 33.3 n_host = np.arange(n_base, n_base + chunk_range, 9, dtype=np.int64)
238 1060 2509267.9 2367.2 49.1 n_dev = cl.array.to_device(queue, n_host)
239 1060 8858.9 8.4 0.2 result_local = cl.LocalMemory(workgroup_size * 8)
240 1060 195368.0 184.3 3.8 sum_dev = cl.array.empty(queue, num_of_workgroups, dtype=np.int64)
241
242 1060 146075.8 137.8 2.9 kernel(queue, n_dev.shape, (workgroup_size,), n_dev.data, result_local, sum_dev.data)
243
244 1060 361061.8 340.6 7.1 sum_host = sum_dev.get()
245 1060 30114.1 28.4 0.6 solution += np.sum(sum_host)
246
247 1 0.4 0.4 0.0 return solution
Generate the Input on the Device #
The great thing about our input is that it’s really just a range of integers in steps of 9. Right now, we’re generating a large array of this sequence, transferring this array to the device, and having each work-item go to its corresponding index to see its assigned value. However, it’s trivial to compute the value at any given index. (base_value + index * 9) This is well within the capabilities of a work-item. So instead, we can have each work-item simply use its global ID to calculate its assigned value.
This is an extremely easy change to make. We only have to change 3 lines in the kernel function.
__kernel void sum_of_valid_solutions(
const long base_n, // The `n` array is replaced with a base scalar value
__local long *result,
__global long *sum)
{
size_t gid = get_global_id(0);
size_t lid = get_local_id(0);
size_t wg_id = get_group_id(0);
size_t wg_size = get_local_size(0);
// Stage 1 - Map
// Compute this work-item's corresponding `n` value
const long n = base_n + gid * 9;
// We now use this private `n` value, instead of accessing an array.
if (is_pandigital(n) && is_substring_divisible(n))
result[lid] = n;
else
result[lid] = 0;
barrier(CLK_LOCAL_MEM_FENCE);
// Stage 2 - Sum
for (uint stride = wg_size / 2; stride > 0; stride >>= 1) {
if (lid < stride)
result[lid] += result[lid + stride];
barrier(CLK_LOCAL_MEM_FENCE);
}
// Store the result
if (lid == 0)
sum[wg_id] = result[lid];
}
Moving towards this method also has a huge impact on the host function. Since we’re only storing the output sum values, our memory requirements are significantly lower. We can do the entire problem in one kernel invocation. We don’t have to operate on the problem space in chunks. Let’s show the math. For our search space of 1,111,111,111 values and a work-group size of 1,024, we will invoke a total of 1,085,070 work-groups. Each work-group only has to return one 64-bit result. This results in a global memory requirement of only 8.28 MB. This is well within the memory limits for my device.
def bruteforce_gpu_custom_sum_best(workgroup_size: int=None, *, platform_id=0, device_id=0) -> np.int64:
# 1_111_111_111 / 1024 is actually 1_085_069.444, so we need
# to add a few extra numbers to the search space to make the
# global size evenly-divisible by the workgroup size.
assert 1_111_111_680 % workgroup_size == 0
num_of_workgroups = np.int32(1_111_111_680 // workgroup_size)
context = cl.create_some_context(interactive=False)
queue = cl.CommandQueue(context)
program = cl.Program(context, open('src/opencl/p43_bruteforce_best.cl').read()).build()
kernel = program.sum_of_valid_solutions
sum_dev = cl.array.zeros(queue, num_of_workgroups, dtype=np.uint64)
result_local = cl.LocalMemory(workgroup_size * 8)
kernel(queue, (1_111_111_680, ), (workgroup_size, ), np.int64(0), result_local, sum_dev.data)
sum_host = sum_dev.get()
return np.sum(sum_host)
Now let’s run this last optimization and see the improvement.
PS > .\measure_performance.ps1
Bruteforce GPU - Custom-built Sum Kernel (Generate All Input on the Device)
Correct solution!
Count : 20
Average : 0.582332535
Sum : 11.6466507
Maximum : 0.7341529
Minimum : 0.5592396
Property :
Pretty phenomenal! That’s over 1000x faster than the original single-threaded solution. Over 190x faster than the optimized CPU multi-processing solution. Over 8x faster than the built-in reduction kernel. And finally, well under Project Euler’s 1-minute rule.
Summary #
I hope this article gave you a decent enough introduction to OpenCL, GPGPU, or parallel programming in general. You can see that even extremely silly uses of GPU computation still gave us some huge performance boosts over just using the CPU. If you ever come across a problem in the future than seems like it could be easily parallelized, take a look at PyOpenCL’s pre-made parallel algorithms. Perhaps you too can achieve a 100-fold performance boost just from using a pre-made algorithm.
| Implementation | Runtime (seconds) | Improvement |
|---|---|---|
| CPU - Single-threaded | 583.07 | - |
| CPU - Multi-processed | 251.79 | 2.3x |
| CPU - Multi-processed (optimized) | 112.65 | 5.2x |
GPU - copy_if Kernel |
8.35 | 69.8x |
GPU - ReductionKernel |
5.05 | 115.5x |
| GPU - Custom Kernel | 56.82 | 10.3x |
| GPU - Custom with Naive Sum | 5.68 | 102.7x |
| GPU - Custom with Naive Sum and Work-Groups | 5.08 | 114.8x |
| GPU - Custom with Parallel Sum | 4.92 | 118.5x |
| GPU - Custom with Input Generated on Device | 0.58 | 1,005.3x |